本文来自微信公众号“开放隐私计算”。
量子计算带来的威胁
安全多方计算和联邦学习作为隐私计算的两条重要实现路径,其协议的安全性主要取决于底层密码算法的安全性。以广泛应用的隐私集合求交(Private Set Intersection,PSI)和联邦学习XGBoost算法为例,当前的PSI协议采用基于RSA或ECC等公钥密码算法,或融合不经意传输(Oblivious Transfer,OT)及不经意伪随机函数(Oblivious Pseudo-RandomFunction,OPRF),并辅以对称密码算法进行构造。
然而,RSA和ECC等公钥密码算法无法满足后量子安全性,已成为后量子时代潜在的安全隐患。另一方面,对于XGBoost来说,目前业界大多利用半同态Paillier算法加密梯度来保证中间传参的隐私性,而Paillier底层仍基于大整数分解困难问题,导致其无法抵御未来量子计算机的攻击。
此外,在可信硬件和密码芯片中,除了诸如证书验证、密钥协商、数字签名等协议因包括公钥密码算法而受到量子计算威胁外,传统密码硬件还提供硬件优化的加密算法指令集,如AES的S盒操作,大整数的模幂运算等。然而,此类硬件优化指令集并不能直接适用于后量子密码,需要在硬件指令集上进行额外调整来适配新的操作,比如数论变换(NumberTheoretic Transform,NTT)及多变量的运算等。
总之,通过后量子密码算法建立满足后量子安全的隐私计算协议,并构建适合于后量子密码的密码芯片或可信硬件,对于保障未来量子计算时代隐私计算技术安全性与可靠性具有十分重要的意义。
后量子密码迁移是保障量子计算时代密码长效安全的有效方法之一,同时也适用于隐私计算技术。以隐私集合求交和XGBoost算法为例,可以将普遍采用的公钥密码算法进行后量子密码算法替换,以提升整个协议的抗量子攻击能力。例如,可以将PSI的OT部分与联邦XGBoost中的Paillier算法用基于格的全同态加密来替代。
当然,实现后量子安全的隐私计算并不仅是简单的算子替换,还涉及整个协议在量子攻击下的可证明安全性分析、相应算法与协议的后量子安全强度及资源消耗量化评估等问题,因而如前所述,后量子密码研究与工程迁移将是一项复杂且持续性任务。
隐私计算作为一项新兴技术,一方面其本身的安全性对于数据要素市场化、国家数据安全的保障具有重要意义;另一方面,相比于其他的传统信息系统,隐私计算系统本身刚起步,迭代空间较大,应用范围也还在逐步扩大,后量子密码迁移对其业务影响相对较小,成本较低,且从业者的认知程度较高,是较为合适的后量子密码迁移实践场景。
当前隐私计算相当一部分算法可以由后量子密码进行高效地实现,未来存在后量子隐私计算形成行业标准的可能。因此,开展后量子隐私计算的研究,对于我国后量子密码领域的相关技术储备、人才储备与标准化都具有十分重要的示范意义。
后量子隐私计算发展
后量子隐私计算是一类由经典计算机执行的隐私计算算法协议簇,可以抵御来自具有量子计算能力的其他参与方或窃听者的密码分析攻击;在量子计算的攻击下,仍能保证参与方私有数据的安全性和隐私性。
构建后量子隐私计算的整体目标是设计并采用既能抵抗量子攻击,又能支持多方协同计算的加密方案和计算协议,保障数据在传输过程以及计算过程中的后量子安全性,实现数据的最小暴露和最大利用。
有效构建后量子隐私计算能力,可遵循以下步骤:首先,使用高效、可靠、安全的后量子密码及数据签名算法,替代或结合现有的基于数论难题的传统密码算法,以确保数据在计算和传输过程中的安全;其次,使用适用于量子计算环境的隐私增强技术,如差分隐私、全同态加密、后量子安全多方计算、后量子联邦学习等,以在量子计算环境下实现数据的“可用不可见”;最后,构建基于后量子密码算法和隐私增强技术的后量子隐私计算框架和平台,为各类应用场景提供可信赖的数据服务。
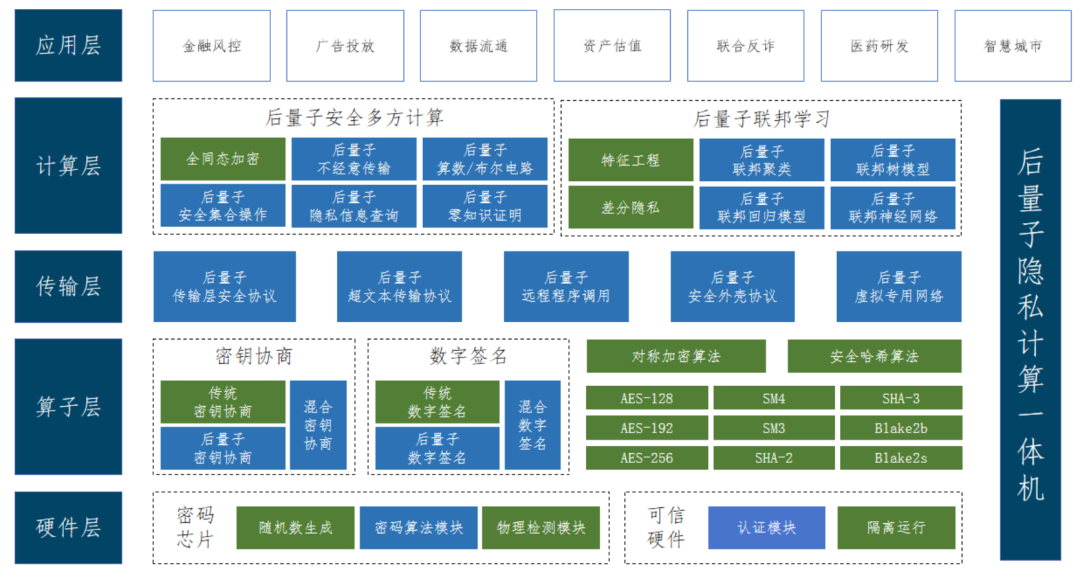
隐私计算体系复杂,覆盖面广,其后量子迁移也需要从多个层面进行框架设计,框架包含硬件层、算子层、传输层、计算层和应用层。无需进行迁移的模块用绿色表示,需要进行改造的模块为蓝色。在硬件层面,研发高效的后量子密码芯片、后量子安全的可信硬件;在算子层面,提供经典的对称密码算子、公钥密码算子和后量子密码算
子;在传输层面,构建后量子的传输层安全协议(Transport Layer Security,TLS)来保证通信安全,能够防范具有量子计算能力的窃听者读取通信数据;在计算层面,研发各种后量子隐私计算算法和协议,如隐私集合求交、隐匿查询、安全电路运算、联邦学习及零知识证明等;在应用层面,基于底层能力开发后量子安全的数据流通实际应用。
这五个层面的协同创新才可确保后量子隐私计算的整体框架基本完整。当前,后量子算法研究、标准化及应用仍处于发展阶段,仍需要政府主管部门的有效引导以及产学研各界共同努力,该后量子隐私计算框架也会随着相关研究的进一步深入而做相应调整。
后量子隐私计算协议优化
利用后量子密码能力构造后量子的数据安全计算方法,让多个参与方在不暴露本身数据的前提下与其他参与方共同完成某个计算任务并得到计算结果。计算层的协议涉及到多个参与方之间频繁的数据传输,其中数据大多以不可恢复的密文形式存在。
后量子安全的计算层的主要目标是提供隐私计算协议的后量子安全版本,在不影响协议功能性的情况下,额外保证其可以抵抗量子计算的攻击。具体来说,计算层包括但不限于以下算法或协议:
1)同态加密
半同态加密(Partially Homomorphic Encryption,PHE)只支持乘法或加法中的一种的同态加密。如Paillier、RSA、ElGamal等。与FHE相比,PHE的复杂性更低,执行速度更快,因此处理速度更快。半同态密码系统标准化较为成熟,如Paillier加密方案已广泛集成到各类数据保护解决方案中。
全同态加密(Fully Homomorphic Encryption,FHE)是一种允许在密文上直接进行任意次数的加法和乘法运算的加密技术。全同态加密算法的核心思想是将明文空间和密文空间之间的运算映射为同态的关系,即在明文空间中相同的运算,在密文空间中也有对应的运算,且解密后计算结果相同(或近似)。FHE可以在不泄露任何关于明文或密钥的信息的前提下保证计算结果的正确性。
FHE的主要挑战是效率问题,为支持无限次数的运算,目前已知的全同态加密方案都需要很高的计算复杂度和存储空间,还存在着噪音增长和密钥管理等问题。但如果只在密文上进行有限次数的运算,现有的(Leveled)FHE可以提供较好的计算效能,因此FHE可以被用于构造一些特定的安全计算协议。
此外,FHE的安全性基于LWE或RLWE困难问题,参数的选取需谨慎。一般来讲,特定参数的FHE方案所提供的安全性要比NIST标准提供的基于LWE的算法要强。因此,FHE是一个构造后量子安全计算协议的优质工具。
2)不经意传输
不经意传输(Oblivious Transfer,OT)是一种基础密码学原语,它允许发送方向接收方传输一些信息,接收方获取其中一部分信息而无法得到任何其他信息。OT有多种变体,例如2选1-OT、n选1-OT、相关OT、随机OT、OT拓展等。向量不经意线性关系(Vector Oblivious Linear Equation,VOLE)允许两个参与方在不泄露任何私密输入的情况下得到一对具有线性关系的向量。
OT和VOLE可以用于实现多种安全的多方计算协议,如隐私求交PSI或通用安全多方计算。后量子OT和VOLE都可以基于后量子安全假设如LWE或偏差学习问题(Learning Parity with Noise,LPN)来构造。通过实现后量子OT和VOLE原语,可以为其他后量子安全计算算法提供基础算子。
3)通用安全多方计算MPC协议
安全多方计算MPC协议是一种允许多个参与者在不泄露各自私密数据的情况下,共同计算一个函数结果的技术。安全多方计算的目标是保证参与者的数据隐私和计算正确性,即使有部分参与者是恶意的。
MPC可以分为通用的MPC协议或特定功能的MPC协议,通用的MPC协议是解决通用的计算问题,可以通过秘密分享、混淆电路等方式构造算数电路或布尔电路来构造。特定功能的MPC协议则包括隐私求交、隐匿查询或零知识证明等特定算法。对于通用的MPC协议,一般来说基于秘密分享的构造在加法和乘法运算上是信息论安全的,多方之间可以通过操作本地数据完成加法或使用乘法三元组来计算秘密分片上面的乘法。
然而生成乘法三元组的过程或计算特定的非多项式运算比如比大小、激活函数、除法等运算需要使用OT或者Paillier算法,可能不满足后量子安全性,因此,后量子的通用MPC需要针对这方面进行改造。
另一方面,混淆电路(GarbledCircuit,GC)的基本思想是将原始的布尔电路转换为一个加密的电路,每个参与者只能看到自己的输入对应的加密值,而不能推断出其他参与者的输入。通过使用OT交换加密值和解密表,参与者可以逐层计算出电路的输出,而不暴露中间结果。对于混淆电路的后量子改造也主要涉及对于OT的替换。
4)隐私集合求交和隐匿查询
隐私集合求交PSI和隐匿查询(Private Information Retrieval,PIR)是两类典型的特定MPC算法。其中,PSI可以让两个或多个参与者安全地计算他们的私有数据集的交集,而不泄露任何额外的信息;PIR是一种允许用户从数据库中检索数据,而不泄露他们检索的内容的技术,PIR的主要动机是保护用户的隐私,防止数据库所有者或其他观察者推断出用户的兴趣或偏好。
PIR有两种基本类型:信息论PIR和计算PIR。信息论PIR可以在不信任数据库所有者的情况下实现完美的隐私,但需要多个不相互通信的数据库副本。计算PIR只需要一个数据库,但依赖于计算困难性假设,如RSA或学习有错误的假设。
PSI和PIR的实现方式有很多,像前文提到的基于RSA、ECC或者基于OT、VOLE的等等。目前行业内应用较多的方案基本都包括公钥密码部分,为满足后量子安全性,需要针对这些公钥模块进行PQC改造。
5)联邦学习
联邦学习FL是一种机器学习方法,允许多个参与者在保持训练数据隐私的同时,协同训练一个模型。FL的基本思想是每个参与者使用自己的本地数据对模型进行更新,随后将更新的模型参数发送给中心服务器或某个计算方。服务器对所有参与者的模型参数进行聚合,得到一个全局的模型,并将其分发给所有参与者。每个参与者都可以从其他参与者的数据中学习,而不需要直接共享原始数据。FL中的数据交互过程需要用(半)同态加密或者秘密分享来加密梯度以保护其隐私性,因此安全性同样容易受到量子计算攻击影响,需要仔细的评估FL中量子脆弱的部分,并进行后量子算法协议的改造。
6)零知识证明
零知识证明(Zero Knowledge Proof,ZK/ZKP)是一类密码学计算协议,其主要特征在于:遵循该协议的证明者可以向验证者证明某个陈述是真实的,而不需要透露任何其他信息。零知识证明的优点是可以保护证明者的隐私,同时也可以防止证明者伪造错误的证明。零知识证明应用领域广泛,例如身份认证、数字签名、资产证明等。在隐私计算中,ZKP常用于将半诚实的安全计算协议扩展为恶意模型安全的协议。现有的ZKP体系大多数基于椭圆曲线密码体系,如何设计量子安全的通用ZKP或采用ZKP增强MPC的安全性仍是一项开放性课题。

